
1. 미분 개념
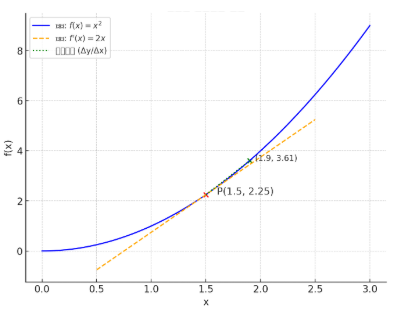
위의 그림은 미분의 기하학적 의미를 설명한 도형입니다.
미분을 간단히 설명하면
"함수 위 어느 한 점에서 접선을 이루는 직선의 기울기 값입니다."
1) 파란 곡선은 함수 f(x)=x2 입니다.
2) 빨간 점은 x=1.5일 때 함수 위의 점 P(1.5,f(1.5))입니다. (기울기)
3) 주황색 점선은 해당 점에서의 접선이며, 이는 f′(x)=2x의 값을 이용해 기울기를 구한 것입니다.
4) 녹색 점선은 두 점을 연결하는 초기할선 (secant line)입니다. 이 선의 기울기는 Δy/Δx, 즉 평균 변화율입니다.
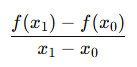
※ 접선 : 곡선상의 두 점 PㆍQ를 연결하는 직선을 가정하고,
점 Q가 이 곡선에 따라 한없이 점 P에 접근할 때의 직선 PQ의 극한의 위치. 또는 그 자취.
▶ 요점
- 미분 f′(x)은 곡선의 한 점에서의 기울기입니다.
- 이는 극한적으로 Δx→0일 때 할선이 접선으로 수렴하는 과정에서 얻어집니다.
- 심박수, 속도 등 실생활에서 변화율을 측정할 때 이 개념이 쓰입니다.
2. 적분 개념
"아주 작은 가로 길이 Δt에 해당하는 직사각형의 높이 f(t)를 곱해 면적을 구하고, 이런 조각들을 전부 더해 전체 면적을 얻는 것"
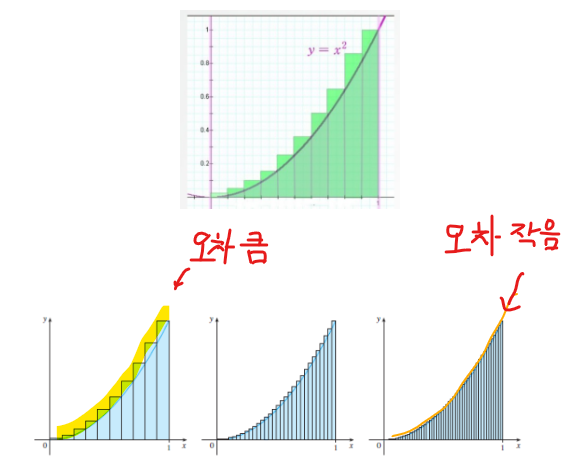
▶ 위 그림에서 함수 y=x2 그래프 아래와 x축 위의 면적을 계산하려면,
① 녹색 직사각형들의 면적을 각각 계산해서 더해 주면된다. (위 그림에서는 10개의 사각형)
② 그리고 오차를 줄이려면 x축 길이를 무한대로 나누어서 무한개의 직사각형의 면적을 계산해서 모두 더하면 된다.
👉 이것이 바로 적분식입니다.
1) 적분의 핵심 개념 : 작은 조각들의 합
① 기본 아이디어
- 함수 f(t)가 시간에 따라 변하는 어떤 양(예: 속도, 칼로리 소모율 등)을 나타낸다고 합시다.
- 이 양을 짧은 시간 동안 조금씩 누적하면 전체 합을 얻을 수 있습니다.
- 적분은 이 무한히 작은 구간들의 합을 의미합니다.
② 수식 표현
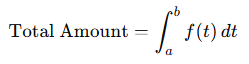
- f(t): 단위 시간당 양(예: 순간 칼로리 소모율)
- a : 시작 시간
- b : 종료 시간
- dt : 매우 짧은 시간 간격
- ∫ : 적분 기호. 무한히 많은 작은 구간의 합을 의미
2) 예시 1: 칼로리 소모량 계산
- C(t) : 시간 t에서의 칼로리 소모율 (단위: kcal/분)
- 하루의 시작과 끝 : t0=0, t1=1440분 (24시간)
- 적분식

➡ 하루 동안 시시각각 달라지는 칼로리 소모율 C(t)를 쌓아가면 전체 칼로리 소모량이 계산됩니다.
3) 예시 2 : 속도와 거리
- v(t) : 시간 t에서의 순간 속도 (단위: m/s)
- 적분하면, 전체 이동 거리
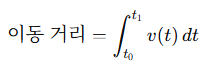
3. 적분과 미분의 관계
1) 미분은 변화량을 구합니다.
→ 예: 위치의 시간에 대한 미분 = 속도
2) 적분은 누적량을 구합니다.
→ 예: 속도의 시간에 대한 적분 = 이동 거리
즉, 적분은 미분의 반대 연산입니다.
'[교육]' 카테고리의 다른 글
| [교육] "미분/적분"으로 만드는 기기 - 내비게이션 (0) | 2025.06.17 |
|---|---|
| [교육] "미분과 적분"은 실생활 어디에 쓰이나 ? 👉 스마트워치, 내비게이션, 주가변동 변화율 예측, 심장박동 변화 분석,.... (6) | 2025.06.13 |
| [교육] 중학교 3학년 '수학을 어디에 쓰나?' 👉 목차별 "사회·산업 활용 분야 총정리" (1) | 2025.06.10 |
| [교육] 중학교 2학년 '수학을 어디에 쓰나?' 👉 목차별 "사회·산업 활용 분야 총정리" (5) | 2025.06.10 |
| [교육] 중학교 1학년 '수학을 어디에 쓰나?' 👉 목차별 "사회·산업 활용 분야 총정리" (2) | 2025.06.09 |